クラスタリングとはデータセットいくつかのサブセットに分割する手法のことを指します。本記事では特に機械学習の1つの手法として使われるクラスタリングについて、クラスタリングとは何か、実施する時の注意点、およびその種類について、クラスタリングの事例やクラスタ数を決めるための考え方なども解説します。
本記事を読めば、クラスタリングが何かの大枠がわかりますので、是非ご一読ください。
▼ ChatGPT活用の企業向け生成AIサービス【無料トライアル予約受付中】
目次
クラスタリングとは
クラスタリングは、データセットを特定のルールに基づいていくつかのグループ（クラスタ）に分類することを指します。特にデータ間の類似度に基づいて、似たものを集めたグループに分ける手法が代表的です。機械学習における「教師なし学習」の一つであり、「クラスタ分析」や「クラスタ解析」と呼ばれることもあります。
そもそも機械学習とは、機械（コンピューター）に学習する機能を持たせる手法あるいは研究分野の一つです。例えば、入力されたデータをもとに、機械（コンピューター）が自動で学習し、データの背景にあるルールやパターンを発見する技術などを含みます。
また、機械学習は「教師あり学習」と「教師なし学習」、「強化学習」の大きく3つに分けられます。
事前に出力データ（正解）を与えた状態で学習をさせる「教師あり学習」に対し、クラスタリングを含む「教師なし学習」は、正解を与えない状態で一連の入力データから、データの背景にある隠れたパターンや構造を見つけ出すという特徴があります。
クラスタリングの活用事例
クラスタリングは、次のような場面で活用されています。
マーケティング施策のための顧客分析
商品・サービスの販売戦略を考える上で、マーケティング活動は欠かせません。例えば、アンケートや市場調査などで得た顧客のデータをクラスタリングすることで、共通点に基づいて顧客をグループ分けする顧客セグメンテーションや、新たなペルソナの発見などに活用できます。
大多数とは振る舞いが異なるデータを抽出する異常検知
異常検知とは、大多数のデータとは振る舞いが異なるデータを検出すること。例えば、画像処理技術とクラスタリングを組み合わせ、ある製品100個の画像データをクラスタリングにかけ、分類されたグループが少数派であれば、異常である可能性があると判断できます。こうした技術は、製造業界や医療業界などで活用されています。
データの前処理
クラスタリングの有名な総説論文『Clustering: Science or Art?』では、クラスタリンの使用例としてデータの前処理をあげています。
機械学習の教師あり学習において実施するラベル付け（アノテーション）にクラスタリングの結果が参考にされることもあります。
例えば、顧客の購買履歴から顧客が好む商品のタイプを予測する分類タスクを考える際、商品の種類が多く商品カテゴリが複雑である場合、アノテーションが非常に困難になります。この場合、クラスタリングを使用することができます。
クラスタリングを使用すると、似たような商品が同じクラスタにまとめられ、クラスタに属する商品の共通点を抽出することができます。これにより、商品の特徴がより明確になり、アノテーションが容易になります。
探索的データ解析（EDA）
『Clustering: Science or Art?』では、クラスタリングの使用例として探索的データ解析（Exploratory Data Analysis：EDA）もあげています。
探索的データ分析とは、データセットを詳しく調べて特徴やパターン、相関関係などの潜在的な情報を明らかにすることをさします。クラスタリングによって、データセット内のパターンやグループを特定し、データのサンプリングや異常値検出、カテゴリ変数のエンコーディングなどのタスクに役立てることができます。
クラスタリングの種類と手法
クラスタリングの種類は、グルーピング方法の違いで「非階層的クラスタリング」と「階層的クラスタリング」に大別できます。
|
クラスタリングの種類 |
非階層的クラスタリング |
階層的クラスタリング |
|---|---|---|
|
概要 |
階層を作らずにグルーピングする |
観測値同士の類似性を「距離」とし、距離の近さごとにクラスタをまとめていく |
|
代表的な手法 |
|
|
|
イメージ |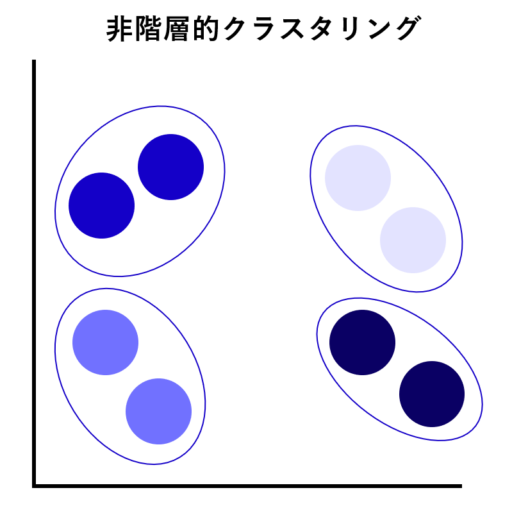
 |
 |
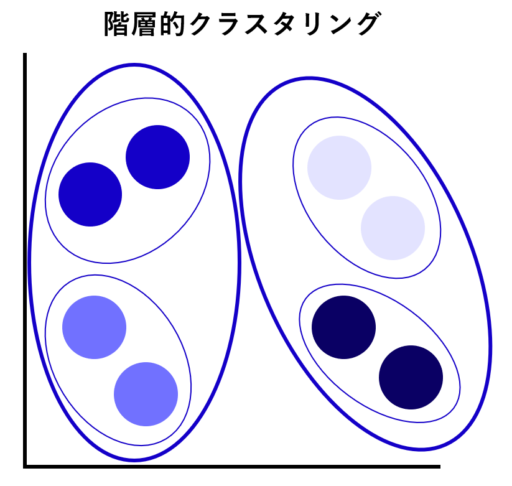それぞれの種類で使われている、代表的な手法を見ていきましょう。
非階層的クラスタリング
「非階層的クラスタリング」とは、階層を作らず、単にグループ分けをするクラスタリングのことを指します。母集団の中で近いデータをまとめ、事前に指定されたクラスタ数に分割します。非階層的クラスタリングには、さらに次の2つの基礎的な手法あります。
k-means法（k-means method）
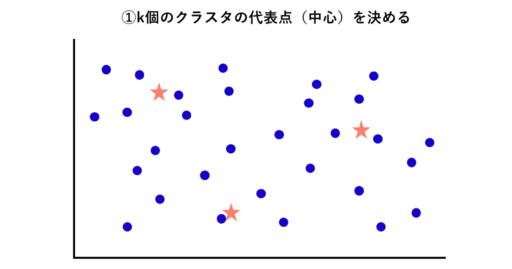
k-means法（＝k平均法）は、最もスタンダードなクラスタリング手法です。入力されているデータの図を例に解説します。
①まず、k個のクラスタの代表点（中心）を決めます。
②次に、全てのデータを、もっとも中心が近いクラスタに振り分けます。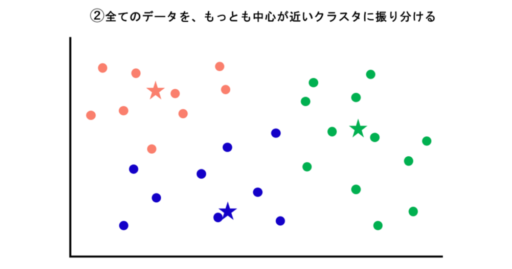
③クラスタがまとまったら、再度、各クラスタの重心点（平均値）を計算しし直します。重心点を変えることでデータが分類されるクラスタも変わります。
④全てのデータのクラスタに変更がなくなるまで③の作業を繰り返し、グループ分けを行います。
以上がk-means法のイメージになります。
混合正規分布（GMM：Gaussian Mixture Model）
左右対称・釣り鐘型の性質をもった確率分布を示すグラフを「正規分布（ガウス分布）」といいます。この正規分布を複数重ねて表現し、クラスタや確率分布を得るのが「混合正規分布（混合ガウス分布）」と呼ばれる手法です。
混合正規分布では、前提として各クラスタに対応する正規分布（ただし多次元）から「データ」が生成されていると仮定します。その上で、そのデータを生成していそうな混合正規分布を推定し、各データ点で「どの正規分布の密度が大きいのか」という視点でクラスタリングを行います。
k-means 法と混合正規分布の違いとして、k-means 法は各インスタンス（データ点）に対して一つのクラスタのみを割り当てるハードなクラスタリング手法です。一方、混合正規分布を使った手法では各インスタンス（データ点）に対して、各クラスタに所属する事後確率を計算するソフトなクラスタリング手法です。
上記の違いがありますが、混合正規分布の代表的な推定アルゴリズムである EMアルゴリズムと k-means のアルゴリズムはある理論的な設定の下では一致することが知られており、本質的には近しい手法となっています。
階層的クラスタリング
階層的クラスタリングは、観測値同士がどのくらい似ているかを「距離」とした場合、距離の近さごとにクラスタをまとめていく手法です。グループ化していく過程は「樹形図（デンドログラム：dendrogram）」で表現でき、可視化される点が特徴です。
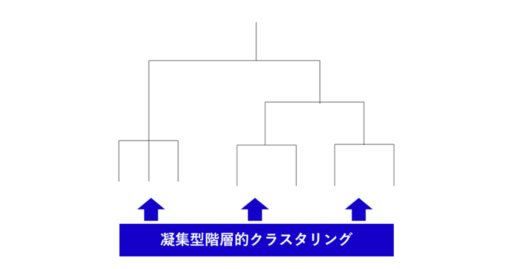
似ているデータを順番にボトムアップ的に結び付けていく手法は「凝集型階層的クラスタリング」と呼ばれます。
※凝集型階層的クラスタリングのイメージ
k-means 法は各インスタンス（データ点）に対して一つのクラスタのみを割り当てるハードなクラスタリング手法です。一方、混合正規分布を使った手法では各インスタンス（データ点）に対して、各クラスタに所属する事後確率を計算するソフトなクラスタリング手法です。
上記の違いがありますが、混合正規分布の代表的な推定アルゴリズムである EMアルゴリズムと k-means のアルゴリズムはある理論的な設定の下では一致することが知られています。つまり、本質的にはかなり近い手法となっています。
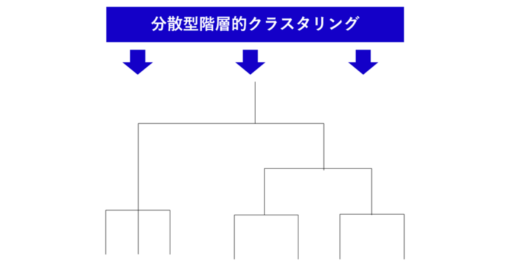
逆に全てのデータを一つの大きなクラスタと定義して類似度が低いデータの組み合わせから小さいクラスタへ分割していく手法を「分散型階層的クラスタリング」と呼びます。
※分散型階層的クラスタリングのイメージ
ウォード法
ウォード法は、各データとの距離の平方和（各データ平均値との差を二乗した値の合計）を算出し、平方和が小さいものから類似度が高いとしてクラスタを作っていく手法になります。計算量が多くなるのが難点ですが、人の直感に合うクラスタリング結果が比較的出やすいため、分析を行う際に最もよく使用されています。
重心法
重心法は、「二つのクラスタそれぞれの重心間の距離」をクラスタ間の距離と定義する手法です。2つのクラスタの重心（平均のデータ）をそれぞれ求め、その重心間の距離が閾値以下となるクラスタを併合していく手順となります。デメリットとして、階層の反転現象が起こることが知られています。この現象が起こると実現したいクラスタリングは難しくなります。
最短（最長）距離法
最短距離法は、「二つのクラスタに含まれるデータのうち、最も近いデータ同士の距離」をクラスタ間の距離と定義する手法です。クラスタを構成するデータ同士の距離を全て計算し、その中で一番距離の短い組み合わせを選び併合していきます。
一方で、最長距離法は、「二つのクラスタに含まれるデータのうち、最も遠いデータ同士の距離」をクラスタ間の距離と定義します。
最短距離法と最長距離法は共に外れ値の影響が大きく出る手法です。特に最短距離法では鎖効果と呼ばれる「ある１つのクラスタに対象が１つずつ吸収されながらクラスタが形成され帯状になる現象」が現れます。これは分類の精度としては低くなり、やりたかったクラスタリングが後段でしづらくなるというデメリットもあります。
群平均法
群平均法は、最短距離法と最長距離法を組み合わせたような手法で「二つのクラスタに含まれる全てのデータ同士の距離の平均」をクラスタ間の距離と定義する手法です。全ての距離の平均を求めるため、クラスタ内に一つだけ離れたデータ（外れ値）があった場合も影響を受けにくいというメリットがあります。ウォード法の方が良い結果を出しやすいと言われていますが、ウォード法よりも計算量も軽いためこちらの結果を見てみても良いでしょう。
階層的クラスタリングと非階層クラスタリングの使い分け
階層的クラスタリングと非階層的クラスタリングのどちらを使えばよいのか検討する際のポイントを二つご紹介します。
データの数
一つ目のポイントは、取り扱うデータの数です。階層的クラスタリングは比較的計算量が大きいため、データ数が数十個程度で少ない場合は「階層的クラスタリング」を、データの数が100を超えてくる場合は「非階層的クラスタリング」を使うのが一般的です。
データに階層構造が馴染むかどうか
二つ目のポイントとして、データに階層構造が馴染むかどうか（良い類似度/非類似度が定義できるかどうか）という点も重要です。もし上手く階層構造を得ることができた場合はそこからクラスタ数を考えるという順番がやりやすい場合もあります。どうしても上手く階層構造が得られない場合は非階層的クラスタリングを行うというケースもあります。
クラスタリングにおけるクラスタ数の考え方
クラスタリングの論点の一つとして、「クラスタ数はいくつが最適か」というクラスタ数の決定問題が挙げられます。前提として、分析をする人が解釈しやすいクラスタ数であることが優先されるべきですが、その上で技術的にクラスタ数を検討する方法について、非階層的クラスタリングと階層的クラスタリングでそれぞれどのような考え方をすればよいか、簡単に説明します。
非階層的クラスタリングの対象数
非階層的クラスタリングのクラスタ数は、数百個あっても問題ありませんが、後段で人が解釈を考える必要が出てくるのであればそれに制限されるため、それを考慮した上で検討しましょう。
階層的クラスタリングの対象数
階層的クラスタリングのクラスタ数は数十個を想定しておくとよいでしょう。あらかじめ数を指定する必要はありません。しかし、対象数が多すぎると計算による負荷が増えることと、後段で人間による解釈を考える必要が出てくるため、それを考慮した数にするようにしましょう。
本記事では細かい解説は割愛しますが、クラスタ数を統計学的アプローチで検討したいという方は以下の手法も参考にしてみてください。
- Calinski-Harabasz index
- Silhouette Analysis
- Gap statistics
- Stability analysis
クラスタリングの注意点
最後に、クラスタリングを行う際の注意点を確認しましょう。
分析の前に仮説を考える
クラスタリングを行う際には、事前に仮説を立てておく必要があります。何も考えずに分析を行った場合、「データが分類された」という事実が残るだけだからです。目的を明確にして仮説を立てた上で、クラスタリングを実行するようにしましょう。
計算に時間がかかる
先述したように、クラスタリングはアルゴリズム中であらゆる組み合わせを検討し、計算を繰り返し行います。そのため、ビッグデータを分析する際など、データサンプル数が多くなった場合は計算量が増え、結果を出すのに時間がかかるというデメリットがあります。
精度の評価が難しい
クラスタリングは精度の評価が難しいともいわれています。使用する手法や変数を少し変えるだけで誤差が生じ、結果が変わってしまうケースがあるためです。複数の初期値や手法を使って同じようなクラスタがあらわるか再現性を検討するとより妥当なクラスタリング結果になるため意識しましょう。
まとめ
クラスタリングは、類似性のあるデータをグルーピングする手段として有効です。複雑なデータをより利用しやすい形に変えられるため、さまざまな分野で活用できるでしょう。まずは、自社においてどのように役立てられるのか考えてみてはいかがでしょうか。実際にクラスタリングを活用してみたい方は、ぜひPythonなどのツールで試してみてください。